Sam Quinns's 2017 honours thesis in mathematics, on "Pivotal categories, matrix units, and towers of biadjunctions", supervised by Tony Licata, Scott Morrison, and Corey Jones, is available here.
Outline
In this thesis we study a tower of biadjunctions coming from a pivotal tensor category with a self dual object. In order to do this, we present some relevant parts of the standard theory of monoidal categories, tensor categories, and pivotal tensor categories. We recall a method for constructing matrix units for the algebras $\operatorname{End}(X^{\otimes n})$ for any object $X$ in a semisimple linear monoidal category.
Using these matrix units, we then prove our main result, Theorem 4.2.14. In a linear monoidal category, endomorphism algebras for tensor powers of a distinguished object $X$ can be used to build a tower of algebras. We prove that when the category is a pivotal tensor category and the object $X$ is self dual, the induction and restriction functors associated to this tower form biadjoint pairs.
Inspired by [Kho14], we use the data of these biadjunctions to construct a graphical category $\mathcal G_X$ . The morphisms in this category are various planar diagrams, modulo some local relations. For instance, one such relation is
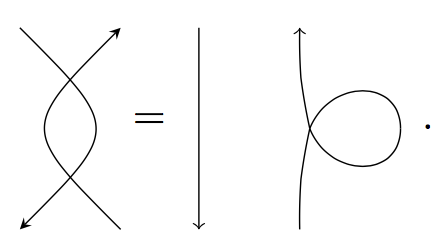
The construction in [Kho14] has been a rich source of interesting mathematics. The hope is that our category might prove to be similarly interesting.